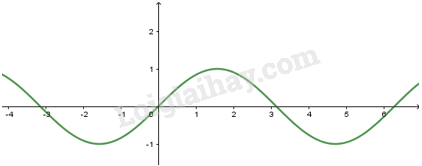
Hàm số y = sin x và hàm số y = cos x

 1. Hàm số y=sinxy=sin⁡x

- Có TXĐ D=RD=R, là hàm số lẻ, tuần hoàn với chu kì 2π2π, nhận mọi giá trị thuộc đoạn [−1;1][−1;1].

- Đồng biến trên mỗi khoảng (−π2+k2π;π2+k2π)(−π2+k2π;π2+k2π) và nghịch biến trên mỗi khoảng (π2+k2π;3π2+k2π)(π2+k2π;3π2+k2π)

- Có đồ thị là đường hình sin đi qua điểm O(0;0)O(0;0)

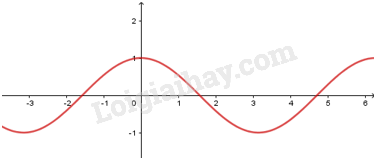
2. Hàm số y=cosxy=cos⁡x

- Có TXĐ D=RD=R, là hàm số chẵn, tuần hoàn với chu kì 2π2π, nhận mọi giá trị thuộc đoạn [−1;1][−1;1].

- Đồng biến trên mỗi khoảng (−π+k2π;k2π)(−π+k2π;k2π) và nghịch biến trên mỗi khoảng (k2π;π+k2π)(k2π;π+k2π)

- Có đồ thị là đường hình sin đi qua điểm (0;1)(0;1)

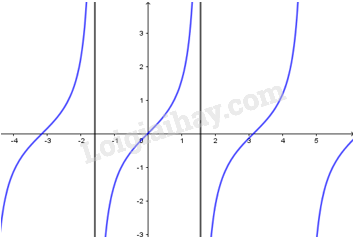
3. Hàm số y=tanxy=tan⁡x

- Có TXĐ D=R∖{π2+kπ,k∈Z}D=R∖{π2+kπ,k∈Z}, là hàm số lẻ, tuần hoàn với chu kì ππ, nhận mọi giá trị thuộc RR.

- Đồng biến trên mỗi khoảng (−π2+kπ;π2+kπ)(−π2+kπ;π2+kπ).

- Đồ thị nhận mỗi đường thẳng x=π2+kπx=π2+kπ làm đường tiệm cận.

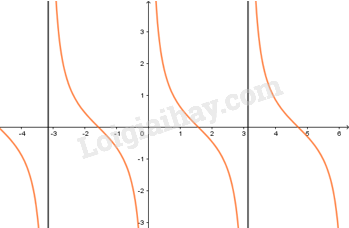
4. Hàm số y=cotxy=cot⁡x

- Có TXĐ D=R∖{kπ,k∈Z}D=R∖{kπ,k∈Z}, là hàm số lẻ, tuần hoàn với chu kì ππ, nhận mọi giá trị thuộc RR.

- Nghịch biến trên mỗi khoảng (kπ;π+kπ)(kπ;π+kπ).

- Đồ thị nhận mỗi đường thẳng x=kπx=kπ làm đường tiệm cận.

Bài giải tiếp theo